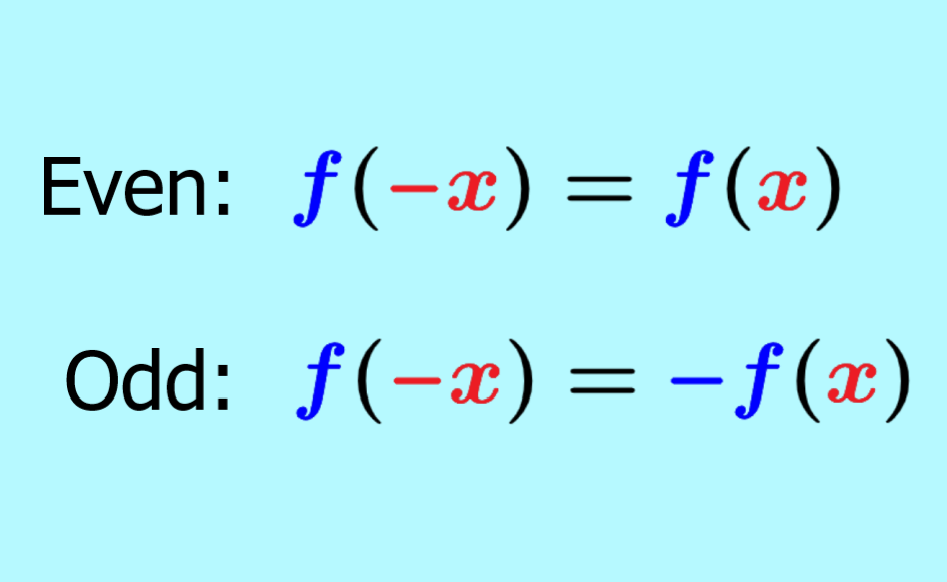Ever wondered why even and odd functions are such a big deal in math? They’re not just random concepts; they’re the backbone of symmetry in mathematics. Whether you're solving equations, graphing functions, or diving into advanced calculus, understanding even odd function properties is crucial. So, buckle up, because we’re about to explore the fascinating world of even and odd functions in a way that’s both simple and mind-blowing.
Picture this: you’re sitting in your math class, staring at a graph that looks like a perfect mirror image. Or maybe it’s flipped upside down. That’s where even and odd functions come in. These functions have unique properties that make them super useful in everything from engineering to physics. But what exactly makes a function even or odd? Stick around, and we’ll break it down step by step.
Before we dive deep, let’s set the stage. Even odd function properties aren’t just about numbers; they’re about patterns and symmetry. And who doesn’t love symmetry? From art to nature, symmetry is everywhere. In math, even and odd functions are like the yin and yang of algebra. They complement each other and help us understand complex problems in simpler terms. Now, let’s get to the nitty-gritty!
Read also:Elizabeth Banks Naked A Candid Look At The Starrsquos Journey Challenges And Legacy
What Are Even Odd Functions?
Let’s start with the basics. Even and odd functions are mathematical functions that exhibit specific symmetry properties. An even function is symmetric about the y-axis, meaning if you fold the graph along the y-axis, both sides match perfectly. On the flip side, an odd function has rotational symmetry about the origin, so if you rotate the graph 180 degrees, it looks the same.
Here’s the kicker: these properties aren’t just theoretical. They have real-world applications. For example, in signal processing, even functions represent symmetric signals, while odd functions represent antisymmetric signals. So, whether you’re designing a bridge or analyzing sound waves, even odd function properties are your best friends.
How to Identify Even Odd Functions
Identifying even and odd functions is simpler than you think. Here’s a quick rundown:
- Even Function: If \( f(-x) = f(x) \) for all \( x \), then the function is even.
- Odd Function: If \( f(-x) = -f(x) \) for all \( x \), then the function is odd.
- Neither: If neither condition is met, the function is neither even nor odd.
Think of it like this: even functions are all about balance, while odd functions are about opposites attracting. And don’t worry if a function doesn’t fit into either category; it’s perfectly normal!
Even Odd Function Properties: The Basics
Now that we know what even and odd functions are, let’s talk about their properties. These properties are the bread and butter of mathematical analysis. Here’s a quick overview:
Property 1: Symmetry
Symmetry is the defining feature of even and odd functions. For even functions, the symmetry is about the y-axis. For odd functions, it’s about the origin. This symmetry makes them incredibly useful in simplifying complex problems. Imagine trying to solve an integral without knowing the symmetry of the function. It’d be like trying to navigate without a map!
Read also:Unveiling Movierulz Telugu Movies 2024 Your Ultimate Guide To Downloading And Streaming
Property 2: Algebraic Behavior
Even and odd functions behave differently under addition, subtraction, and multiplication. Here’s how:
- The sum of two even functions is even.
- The sum of two odd functions is odd.
- The product of two even functions is even.
- The product of two odd functions is also even.
- The product of an even and an odd function is odd.
These rules might sound complicated, but once you get the hang of them, they’re a piece of cake. It’s like learning the rules of a game; once you know them, you can play like a pro!
Applications of Even Odd Function Properties
So, why should you care about even odd function properties? Because they’re everywhere! From physics to engineering, these properties have countless applications. Here are a few examples:
Application 1: Fourier Series
In Fourier analysis, even and odd functions play a crucial role. Fourier series are used to represent periodic functions as a sum of sine and cosine waves. Even functions are represented by cosine terms, while odd functions are represented by sine terms. This decomposition is essential in signal processing, image compression, and more.
Application 2: Calculus
Even odd function properties make calculus a lot easier. For example, when calculating definite integrals, knowing whether a function is even or odd can simplify the process. If a function is even, the integral from \(-a\) to \(a\) is twice the integral from \(0\) to \(a\). If it’s odd, the integral is zero. Who wouldn’t want to save time on their math homework?
Application 3: Physics
In physics, even and odd functions are used to describe wave motion, electric fields, and more. For instance, the electric potential due to a dipole is an odd function, while the potential due to a monopole is even. Understanding these properties helps physicists model real-world phenomena accurately.
Common Examples of Even Odd Functions
Let’s look at some common examples of even and odd functions. These examples will help you visualize the concepts better.
Example 1: Even Functions
Some classic examples of even functions include:
- \( f(x) = x^2 \)
- \( f(x) = \cos(x) \)
- \( f(x) = |x| \)
Notice how these functions are symmetric about the y-axis. It’s like looking in a mirror!
Example 2: Odd Functions
On the other hand, odd functions include:
- \( f(x) = x^3 \)
- \( f(x) = \sin(x) \)
- \( f(x) = x \)
These functions are all about rotational symmetry. Flip them upside down, and they look the same.
Graphical Representation of Even Odd Functions
Visualizing even and odd functions is key to understanding them. Let’s take a look at how they appear on a graph.
Graph of an Even Function
An even function’s graph is symmetric about the y-axis. For example, the graph of \( f(x) = x^2 \) is a parabola that opens upwards. If you fold the graph along the y-axis, the two sides match perfectly. It’s like a perfect hug from both sides!
Graph of an Odd Function
An odd function’s graph has rotational symmetry about the origin. For example, the graph of \( f(x) = x^3 \) looks like a curve that passes through the origin. If you rotate the graph 180 degrees, it looks exactly the same. It’s like a dance move that works in both directions!
Advanced Topics in Even Odd Function Properties
Now that we’ve covered the basics, let’s dive into some advanced topics. These topics might seem complex, but they’re just extensions of the fundamental properties we’ve discussed.
Topic 1: Even Odd Decomposition
Any function can be decomposed into its even and odd parts. This is done using the formulas:
- \( f_{even}(x) = \frac{f(x) + f(-x)}{2} \)
- \( f_{odd}(x) = \frac{f(x) - f(-x)}{2} \)
This decomposition is useful in many areas, including signal processing and control systems. It’s like breaking down a complex problem into simpler parts!
Topic 2: Complex Functions
Even odd function properties also apply to complex functions. For example, the real part of a complex function is even, while the imaginary part is odd. This property is used extensively in electrical engineering and quantum mechanics.
Tips for Mastering Even Odd Function Properties
Mastering even odd function properties takes practice. Here are a few tips to help you along the way:
TIP 1: Practice, Practice, Practice
The more problems you solve, the better you’ll get. Start with simple examples and gradually move to more complex ones. Don’t be afraid to make mistakes; they’re part of the learning process.
TIP 2: Visualize the Graphs
Graphing functions is a powerful tool. Use graphing calculators or software to visualize even and odd functions. Seeing is believing!
TIP 3: Connect to Real-World Applications
Understanding the applications of even odd function properties will make the concepts more relatable. Whether it’s physics, engineering, or music, there’s always a real-world connection.
Conclusion
In conclusion, even odd function properties are more than just mathematical concepts. They’re tools that help us understand the world around us. From symmetry in nature to symmetry in math, these properties are everywhere. So, whether you’re a student, a teacher, or a professional, mastering even odd function properties will open up new doors of understanding.
Now, it’s your turn! Take what you’ve learned and apply it to your own problems. And don’t forget to share this article with your friends and colleagues. Together, we can make math more accessible and fun for everyone. Until next time, keep exploring and keep learning!
Table of Contents
- What Are Even Odd Functions?
- How to Identify Even Odd Functions
- Even Odd Function Properties: The Basics
- Applications of Even Odd Function Properties
- Common Examples of Even Odd Functions
- Graphical Representation of Even Odd Functions
- Advanced Topics in Even Odd Function Properties
- Tips for Mastering Even Odd Function Properties
- Conclusion